学习笔记

博主： boren
发布时间：2022 年 07 月 25 日
1268 次浏览
暂无评论
2437字数
分类：默认分类

## 工业机器人的机械结构：运动链

工业机器人的驱动源通过传动部件来驱动关节的移动或转动，从而实现机身、手臂和手腕的运动。**目前工业机器人广泛采用的机械传动装置是减速器。**

### 摆线针轮行星传动和渐开线少齿差行星齿轮传动

摆线针轮行星传动和渐开线少齿差行星齿轮传动，同属K-H一行星齿轮传动，其工作原理和结构基本相同。所不同的是，摆线针轮行星传动的行星齿轮的齿廓曲线不是渐开线，而是采用变幅外摆线的内侧等距曲线(其中用短幅外摆线的等距曲线较普遍);太阳轮齿廓与上述曲线共轭的是圆。

# 工业机器人运动学/Kinematics of Industrial Robot

- 坐标系之间的运动关系可以用矩阵之间的乘法运算来表达。
- 简单的运动用一个变换矩阵来表示，则多次运动可用多个变换矩阵的积来表示，表示这个积的矩阵就为齐次变换矩阵。
- 逆向运动学是工业机器人控制的基础（根据工作任务要求确认手部要达到的目标位姿，逆向求出关节变量），正向运动学又是逆向运动学的基础（控制器以求出的关节变量为目标值，对各关节驱动元件发出控制命令，驱动关节运动，使手部到达并呈现目标位姿）

## 前言

![picture 1](https://s2.loli.net/2022/07/22/SJiQWl4ABxzb8Iw.png)

#### 正交矩阵

称n阶方阵A是正交矩阵，若$A^TA=I$，则$A$为正交矩阵，性质如下：

1. A的逆等于A的转置，即$A^{-1}=A^T$
2. A的行列式为±1，$|A|=\pm1$
3. A的行（列）向量组为n维单位正交向量组

- 凡是正交矩阵，一定可以对角化。

# 工业机器人动力学

## 概要

动力学研究两类问题

1. 已知机器人各关节的作用力矩（或力）时，求解机器人的运动轨迹，即**正动力学分析问题**；（求解困难，运算时间长）
2. 已知机器人运动轨迹，求解所需要的关节驱动力矩（或力），即**逆动力学分析问题**。（只对逆动力学进行详细分析）
   **分析方法**：拉格朗日力学原理，因为拉格朗日法能以最简单的形式求得非常复杂的系统的动力学方程。

推导机械臂的动力学方程可按下述五个步骤进行：

1. 计算机械臂任意连杆上任意一点的速度
2. 计算它的动能
3. 推导势能
4. 形成拉格朗日算子
5. 对拉格朗日算子进行微分得到动力学方程

# 齐次坐标变化

## 点向量的描述

p在E坐标系中表示为$^Ep$，在H坐标系中表示为$^Hu$，且![]()。一个点向量可以表示为: $v=a\vec{i}+b\vec{j}+c\vec{k}$

![]()

通常用（n+1）维列矩阵表示，最后一个元素是比例因子w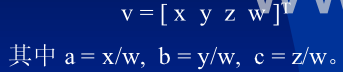

![image.png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image.png)

![image(1).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(1).png)

### 平面

平面用行矩阵表示

$p=[a\ b\ c\ d]$

表示了平面p的法线方向，且距坐标原点的距离为 $-\frac{d}{m}$，其中$m=\sqrt{a^2+b^2+c^2}$

## 变换

空间变换的矩阵为4×4的矩阵。点变换采用在点坐标矩阵左乘变换矩阵，面变换则在面矩阵右乘变换矩阵的逆矩阵。

## 平移变换

![image(2).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(2).png)

## 旋转变换

![image(3).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(3).png)

## 坐标系

空间坐标系的矩阵用4×4的方阵表示，空间坐标系中有3个轴$x,y,z$，矩阵的前三列表示局部坐标系的各个轴的方向，从左到右依次为$x,y,z$轴，最后一列表示世界坐标系下原点在局部坐标系下的坐标。最后一行一般为$[0\ 0\ 0\ 1]$

齐次变换矩阵 $H$ 右四个列向量组成，前三个列向量为方向向量，由旋转变换确定；第四列为平移向量，由平移变换的第四列的前三个元素确定。

$H$变换矩阵描述了一个坐标系绕原参考坐标系旋转和对参考坐标系平移的三个轴的方向和原点的位置。当一个向量进行了H变换时，原向量n可以被认为是在新坐标系描述的那个向量u，即变换了的向量u是相对于参考坐标系描述的同一个向量n。

![image(4).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(4).png)

## 相对变换

一般的情况下，如果我们用一个旋转和／或平移变换矩阵右乘一个坐标系的变换，那么产生的平移和／或旋转是相对于前一个变换的坐标系（当前坐标系）的轴来说的。如果我们用一个描述平移和／或旋转的变换矩阵左乘一个坐标系的变换，那么产生的平移和／或旋转是相对于基坐标系来说的。

## 逆变换

![image(5).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(5).png)

## 一般旋转变换

最后修改：2022 年 07 月 25 日

如果觉得我的文章对你有用，请随意赞赏

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

评论 *

私密评论

名称 *

🎲

邮箱 *

地址

学习笔记

boren • 2022 年 07 月 25 日

## 工业机器人的机械结构：运动链

### 摆线针轮行星传动和渐开线少齿差行星齿轮传动

# 工业机器人运动学/Kinematics of Industrial Robot

## 前言

![picture 1](https://s2.loli.net/2022/07/22/SJiQWl4ABxzb8Iw.png)

#### 正交矩阵

称n阶方阵A是正交矩阵，若$A^TA=I$，则$A$为正交矩阵，性质如下：

1. A的逆等于A的转置，即$A^{-1}=A^T$
2. A的行列式为±1，$|A|=\pm1$
3. A的行（列）向量组为n维单位正交向量组

- 凡是正交矩阵，一定可以对角化。

# 工业机器人动力学

## 概要

动力学研究两类问题

推导机械臂的动力学方程可按下述五个步骤进行：

1. 计算机械臂任意连杆上任意一点的速度
2. 计算它的动能
3. 推导势能
4. 形成拉格朗日算子
5. 对拉格朗日算子进行微分得到动力学方程

# 齐次坐标变化

## 点向量的描述

p在E坐标系中表示为$^Ep$，在H坐标系中表示为$^Hu$，且![]()。一个点向量可以表示为: $v=a\vec{i}+b\vec{j}+c\vec{k}$

![]()

通常用（n+1）维列矩阵表示，最后一个元素是比例因子w

![image.png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image.png)

![image(1).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(1).png)

### 平面

平面用行矩阵表示

$p=[a\ b\ c\ d]$

表示了平面p的法线方向，且距坐标原点的距离为 $-\frac{d}{m}$，其中$m=\sqrt{a^2+b^2+c^2}$

## 变换

空间变换的矩阵为4×4的矩阵。点变换采用在点坐标矩阵左乘变换矩阵，面变换则在面矩阵右乘变换矩阵的逆矩阵。

## 平移变换

![image(2).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(2).png)

## 旋转变换

![image(3).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(3).png)

## 坐标系

齐次变换矩阵 $H$ 右四个列向量组成，前三个列向量为方向向量，由旋转变换确定；第四列为平移向量，由平移变换的第四列的前三个元素确定。

![image(4).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(4).png)

## 相对变换

## 逆变换

![image(5).png](https://yzhyy.oss-cn-shanghai.aliyuncs.com/yu520/2022/07/25/image(5).png)

## 一般旋转变换

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

学习笔记

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款