有限元课后习题——十三章

boren

2020 年 12 月 01 日

2020 次浏览

暂无评论

1779字数

课程相关

## 推导8节点矩形单元的协调质量阵、集中质量

密度为p、单位厚度，集中质量阵分别按式（1）和（2）两种方法推导

$$
\text { (1) } \quad\left(\boldsymbol{M}_{l}^{e}\right)_{i j}=\left\{\begin{array}{ll}
\sum_{k=1}^{n_{e}}\left(\boldsymbol{M}^{e}\right)_{i k}=\sum_{k=1}^{n_{e}} \rho \boldsymbol{N}_{i}^{T} \boldsymbol{N}_{k} d V & (j=i) \\
0 & (j \neq i)
\end{array}\right.
$$

$$
\text { (2) } \quad\left(\boldsymbol{M}_{l}^{e}\right)_{i j}=\left\{\begin{array}{ll}
a\left(\boldsymbol{M}^{e}\right)_{i i}=a \int_{V^{e}} \rho \boldsymbol{N}_{i}^{T} \boldsymbol{N}_{i} d V & (j=i) \\
0 & (j \neq i)
\end{array}\right.
$$

$$
\sum_{i=1}^{n_{e}}\left(\boldsymbol{M}_{l}^{e}\right)_{i i}=a \sum_{i=1}^{n_{e}}\left(\boldsymbol{M}^{e}\right)_{i i}=W \boldsymbol{I}_{d}=\rho V_{e} \boldsymbol{I}_{d}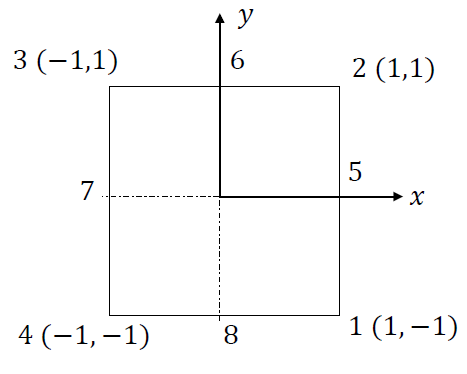
$$

![节点分布](https://yzhyy.oss-cn-shanghai.aliyuncs.com/img/20201201225845.png)

MATLAB代码

```MATLAB
% 题目如图：https://yzhyy.oss-cn-shanghai.aliyuncs.com/img/20201201182007.png
% 计算8节点矩形单元的协调质量阵、集中质量，密度为rho，单位厚度，计算中为加rho，因此M1,M2,M3,都需要在前面点乘rho
% M1为协调质量阵，M2为集中质量阵的第一种算法，其中每一行的主元素等于M1中该行所有元素之和，而非主元素为零
% M3为集中质量阵的第二种算法，其中每一行的主元素等于M1中该行主元素乘以缩放因子a，而非主元素为零。

format rat;
syms xi eta;
N5 = 0.5*(1+xi)*(1-eta^2);
N6 = 0.5*(1+eta)*(1-xi^2);
N7 = 0.5*(1-xi)*(1-eta^2);
N8 = 0.5*(1-eta)*(1-xi^2);
N1 = 0.25*(1+xi)*(1-eta)-0.5*N8-0.5*N5;
N2 = 0.25*(1+xi)*(1+eta)-0.5*N5-0.5*N6;
N3 = 0.25*(1-xi)*(1+eta)-0.5*N6-0.5*N7;
N4 = 0.25*(1-xi)*(1-eta)-0.5*N7-0.5*N8;
N = [N1,0,N2,0,N3,0,N4,0,N5,0,N6,0,N7,0,N8,0;0,N1,0,N2,0,N3,0,N4,0,N5,0,N6,0,N7,0,N8];
M1 = int(int(N'*N,-1,1),-1,1)
MID = zeros(16,1);
for i = 1:16
    for j = 1:16
        MID(i) = MID(i) + M1(i,j);
    end
end
M2 = diag(MID)
TR_M1 = trace(M1);
b =  sum(sum(M1));
a = b/TR_M1; %a根据质量守恒计算，a等于M1的所有元素之和除以M1的主对角线元素之和
M3 = a.*diag(diag(M1))
```

最后修改：2021 年 03 月 03 日

如果觉得我的文章对你有用，请随意赞赏

有限元课后习题——十三章

boren • 2020 年 12 月 01 日

发表评论 取消回复 使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款

有限元课后习题——十三章

发表评论取消回复
使用cookie技术保留您的个人信息以便您下次快速评论，继续评论表示您已同意该条款